진법 변환과 컴퓨터의 사칙연산

전에 컴퓨터의 2진수 사용과 아스키코드에 대해 포스팅했다. 

이번에는 컴퓨터의 진법 변환에 대해 이야기해보려 한다.

 

8bit = 전선 8가닥 = 1byte

앞서 포스팅했듯 컴퓨터는 전기의 OFF/ON 상태를 기반으로 2진법을 사용한다.

0과 1의 두 가지 상태를 나타내는 단위를 bit라고 한다.

 

0과 1 (1bit)의 단순함을 모아 정교하게 만들어 전자식 컴퓨터의 원리를 갖는다.

이때 1bit의 다른 말은 전선 한 가닥이다. 전선 가닥을 부르는 용어가 bit라는 것이다. 

예를 들어 10010110(2)는 8bit로, 전선 8가닥을 의미한다.

사진 출처 https://core-electronics.com.au/8-position-dip-switch.html

 

8개의 bit를 묶은 byte 단위는 컴퓨터가 데이터를 저장하는 최소 단위다.
1byte는 영문 한글자를 담을 수 있는 기억공간의 크기다.

 

 

진법 변환

인간과 기계의 숫자표현을 정리해보면 아래와 같다. 숫자 표기 방법이 다르니 진법 변환을 알아보자.

/* 인간 ******* 컴퓨터 ******* C언어 */    
150(10) == 1001 0110(2) == 0x03(16)

 

2진수 -> 10진수

2진수 10010110(2)는 각 자리수마다 2^0 ~ 2^7 만큼의 가중치(8bit 단위일 때)로 계산하면 10진수 150(10)로 바뀐다.

1	0	0	1	0	1	1	0
1 x 2^7	0 x 2^6	0 x 2^5	1 x 2^4	0 x 2^3	1 x 2^2	1 x 2^1	0 x 2^0
150

 

 

2진수 -> 16진수

컴퓨터는 전기신호로 작동하여 2진법 체계를 갖지만, 2진수로 정보를 표기하면 자릿수가 너무 길어 데이터 분석에 용이하지 않다.

따라서 16진수로 컴퓨터 기계정보를 표기하며, 16진수를 사용하면 보다 상세한 표기가 가능해진다.

16진수 변환은 간단하게 4bit씩 끊어 계산하면 된다.

 

2진수 10010110(2)를 16진수로 바꾸면 0x96(16)이 되며, 16진수라는 구분을 하기 위해 숫자 앞에 0x를 붙여준다.

1	0	0	1		0	1	1	0
1 x 2^3	0 x 2^2	0 x 2^1	1 x 2^0		0 x 2^3	1 x 2^2	1 x 2^1	0 x 2^0
9					6

 

2진법에서는 0~1의 숫자를 사용하고, 2가 되면 자리올림이 발생한다.

10진법에서는 0~9의 숫자를 사용하고, 10이 되면 자리올림이 발생한다.

16진수에서는 0~F의 숫자와 문자를 사용하고 F 이상이 되면 자리올림이 발생한다.

 

0~15까지의 숫자를 사용한다면 아라비아숫자(0부터 9까지)로는 1자리 표기가 불가능하여 자릿수 구분이 안 된다.

따라서 10 이상의 숫자는 알파벳으로 매핑하여 1자리씩 표기할 수 있다.

10 - A | 11 - B | 12 - C | 13 - D | 14 - E | 15 - F

 

2진수 -> 8진수

8진수 변환은 3bit씩 끊어 계산하면 된다.

2진수 10010110(2)를 8진수로 바꾸면 263(8)이 된다.

맨 앞 모자라는 부분은 0으로 채워준다.

0	1	0		1	1	0		0	1	1
0 x 2^2	1 x 2^1	0 x 2^0		1 x 2^2	1 x 2^1	0 x 2^0		0 x 2^2	1 x 2^1	1 x 2^0
2				6				3

 

 

컴퓨터의 사칙연산

컴퓨터의 사칙연산이 어떻게 구현되는가는 다음과 같다.

사칙연산	구현방법
더하기	전가산기로 가능
빼기	보수 더하기
곱하기	왼쪽 Shift
나누기	오른쪽 Shift

구현방법을 이해하기 위해 게이트회로, 전가산기, 보수, 시프트를 아래에서 살펴보자.

 

 

게이트회로

컴퓨터는 아래의 게이트회로 부품 4개를 이용해서 만들어진다.

cpu와 ram 모두 이 4개의 부품으로 만들 수 있다.

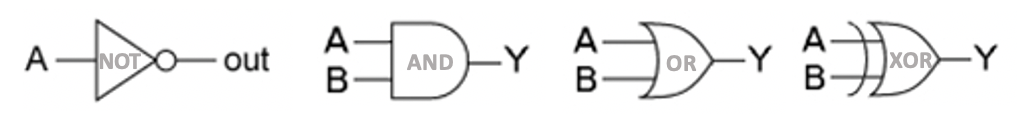
맨 첫 번째 게이트회로는 NOT인데, 다른 말로 Inverter라고 해서 0을 넣으면 1, 1을 넣으면 0을 출력한다.

여기서 0은 전기가 흐르지 않는 상태(Off, False)를 의미하고, 1은 전기가 흐르는 상태(On, True)를 의미한다는 걸 기억하자.

 

나머지 AND, OR, XOR 논리회로의 진리표는 아래와 같다.

입력(In)은 2개이며, 출력(Out)은 1개다.

AND는 논리곱으로서, 두 조건을 만족하는 경우에만 1을 출력한다.

OR는 둘 중 하나만 만족하면 1을 출력한다.

XOR는 두 입력이 서로 다른 경우에만 1을 출력한다.

 

 

AND 논리 게이트회로가 4개 들어간 반도체를 7408 iC회로라고 한다.

iC회로는 컴퓨터 기억소자인데 아래 그림은 3세대쯤 된다.

그림 원본 출처 https://www.electronics-tutorials.ws/logic/logic_2.html?epik=dj0yJnU9blFiT2xQZDFLWW5FMDJOT2dMQ0tsUS10WGg0eklpX2wmcD0wJm49MTVDc1Vtb0V5T0k2OE5HWmppYjFDUSZ0PUFBQUFBR0FRNzVR

두 개의 입력을 받아 한 개의 출력을 출력한다. 즉, 전선 2가닥으로 전기를 입력하면 전선 1가닥으로 전기가 출력된다.
AND 게이트회로이므로 입력 시 한 가닥에 전기를 넣지 않으면 출력으로 전기가 나오지 않는다. (=반도체)

 

 

반가산기의 구성

2개의 전선을 접합해서 연결한 반가산기의 구성은 아래와 같다. 반가산기 회로를 만들면 더하기가 된다.

여기서 입력 A, 입력 B, 출력 (S), 자리올림수 출력(C)의 관계를 의미한다.

 

 

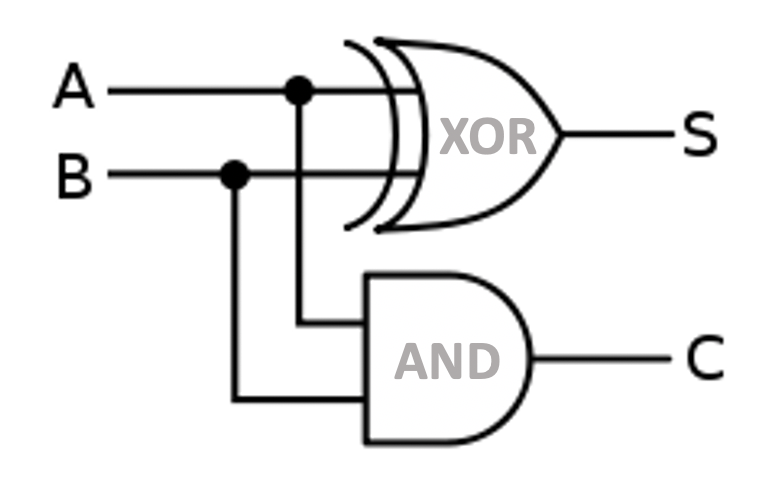
반가산기의 진리표는 다음과 같다.

 

예를 들어 전선 1개에 1bit의 입력을 줬다고 생각해보자.

2진수 1자리끼리 더해서 2자리로 표현할 수 있게 됐다. 즉, 1(2) + 1(2) = 10(2) 이 된다.

S는 현재 자리의 계산결과다.

위의 그림은 최대 표현 가능한 수가 2다. 그 이상으로 101(2) + 101(2) 해서 1010(2) 연산 같은 건 불가능하다.

 

한편, 반가산기의 문제는 자리올림의 개념을 이해하지 못한다는 점이다.

숫자 2개를 더하는데 총 숫자 3개의 덧셈이 이뤄져야 하는데 반가산기는 2개만 더할 뿐이다.

이러한 논리의 한계를 극복하기 위해 입력을 계산할 때 숫자 3개가 더해지도록 전가산기를 사용한다. 

 

 

전가산기 및 4bit Adder의 구성

하나의 전가산기는 두개의 반가산기와 하나의 OR로 구성된다.

입력이 3개 존재해서 (입력 A, 입력 B, 자리올림수 입력) 자리올림을 수행할 수 있다.

 

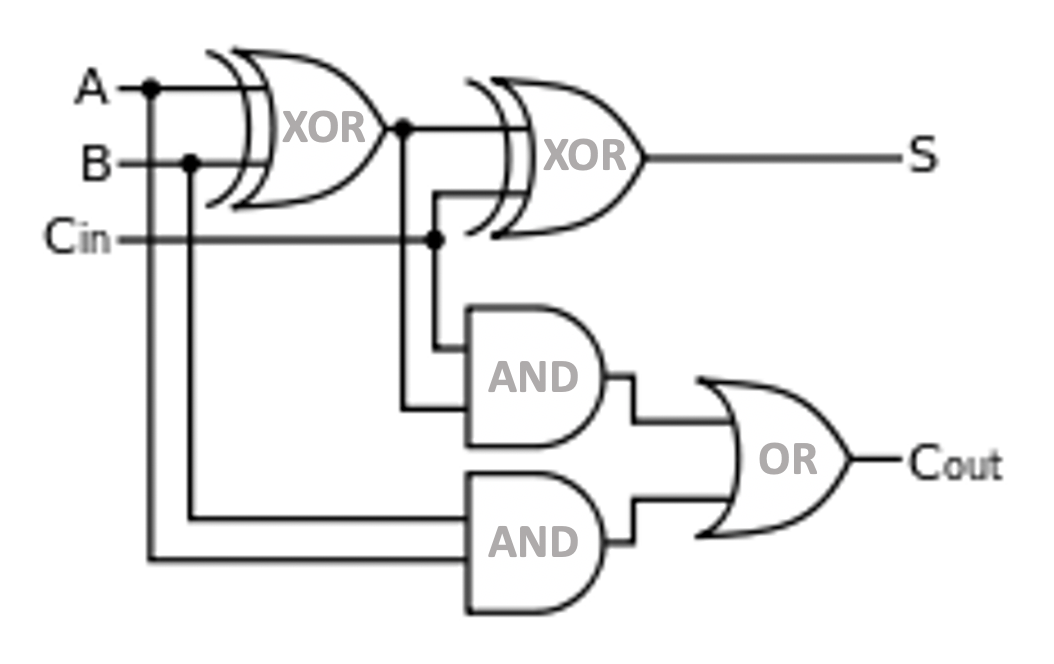
전가산기의 진리표는 아래와 같다.

 

 

다음 그림은 1bit 전가산기의 결선도 기호를 4개 합친 4bit Adder다.

4bit Adder를 사용하면 4bit에 해당하는 4자릿수의 2진수를 더할 수 있다.

거창해보이지만 단순하니 예제를 통해 계산해보겠다.

그림 출처 https://microcontrollerslab.com/cd4008-4-bit-full-adder-ic-pinout-features-example-datasheet/ 

 

 

예를 들어 1011(2) 와 0001(2) 를 더해보겠다.

숫자 1011(2)를  한자리씩 나누어 1, 0, 1, 1 씩 입력하는 것이다.

또한 0001(2)도 한자리씩 쪼개서 0, 0, 0, 1 씩 입력한다. 

두 수를 A와 B로 표시하면 아래와 같다. 첫 번째 자리올림은 없으니 0으로 대체한다.

 

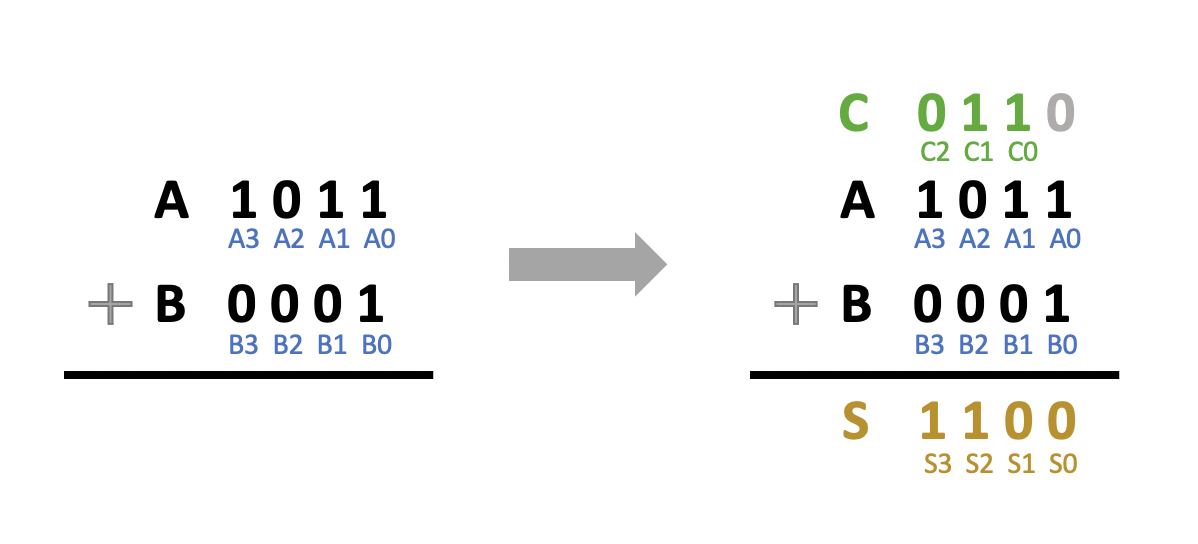
위의 계산식을 4bit Adder로 표기해보자.

각 1bit 전가산기마다 한 자리의 A, B, C의 인풋을 넣으면 된다.

오른쪽부터 계산하여 발생한 자리올림수 C를 왼쪽 가산기로 넘겨주는 방식이다.

덧셈 출력값은 1100(2)인데, 컴퓨터는 최종표기를 16진수인 C(16)로 할 것이다.

컴퓨터에서 더하기가 됐다는 건 가장 기초적인 산술이 됐다는 것인데, 재밌는 건 빼기도 더하기로 구현한다.

 

 

보수와 뺄셈

컴퓨터는 보수의 덧셈을 통해 뺄셈을 구현한다.

뺄셈을 10진수로 나타낸다면 다음과 같다.

6을 뺄셈한다면 10의 보수인 4를 더하고 10을 뺀다. 즉, 발생하는 자리올림을 무시한다.

 

보수의 덧셈에 있어 진법 상의 차이는 없다.

16진수라면 16의 보수를 더하고 발생하는 자리올림을 무시하면 된다.

 

 

Shift와 곱셈, 나눗셈

곱셈은 왼쪽으로 Shift하는 것, 나눗셈은 오른쪽으로 Shift하는 것을 의미한다.

예를 들어 3 * 2(10)를 수행하고 싶다면 2진수로 나타낸 3을 왼쪽으로 시프트하면 된다.

 

또한 8 / 2(10)의 나눗셈을 수행하고 싶다면 2진수로 나타낸 8을 오른쪽으로 시프트한다.

 

 

지금까지 컴퓨터 기본지식인 진법 변환과 사칙연산을 알아보았다.

---

출처

전체적인 내용

유투브 프리렉 최호성 강사님 <C언어를 배우기 전에 알아야할 것들 (1)~(2)> youtu.be/V_oM9ePJyP8

 

반가산기, 전가산기

위키피디아 가산기 ko.wikipedia.org/wiki/%EA%B0%80%EC%82%B0%EA%B8%B0