[딥러닝의 기본] Linear Regression cost 함수 최소화

ML lec 03 - Linear Regression의 cost 최소화 알고리즘의 원리 설명

가설과 실제 값의 차를 최소화할 수 있는 W와 b를 찾는 것이 Linear Regression의 목표다.

 

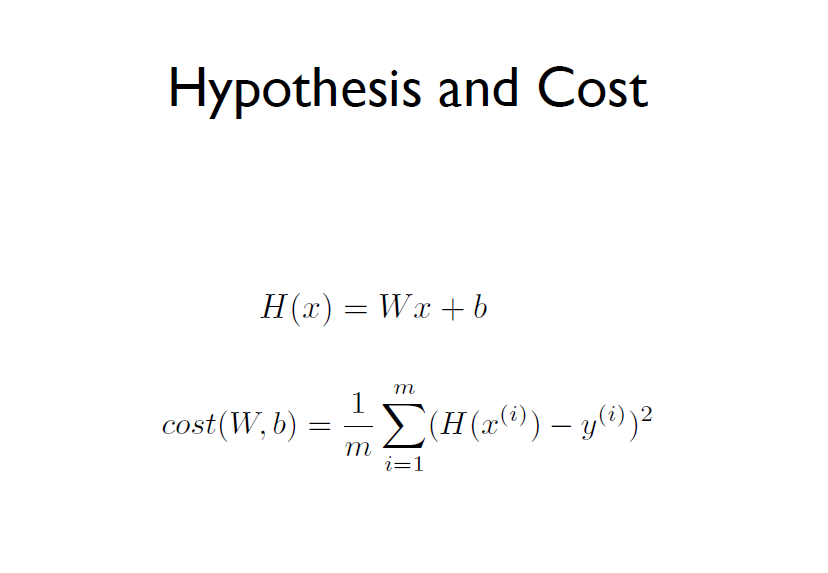
설명을 위해서 hypothesis를 간단히 했다.
편향 b를 없애고 가중치 W만 가진다.

 

W 값에 따라 cost 함수는 어떻게 될지 본다.

 

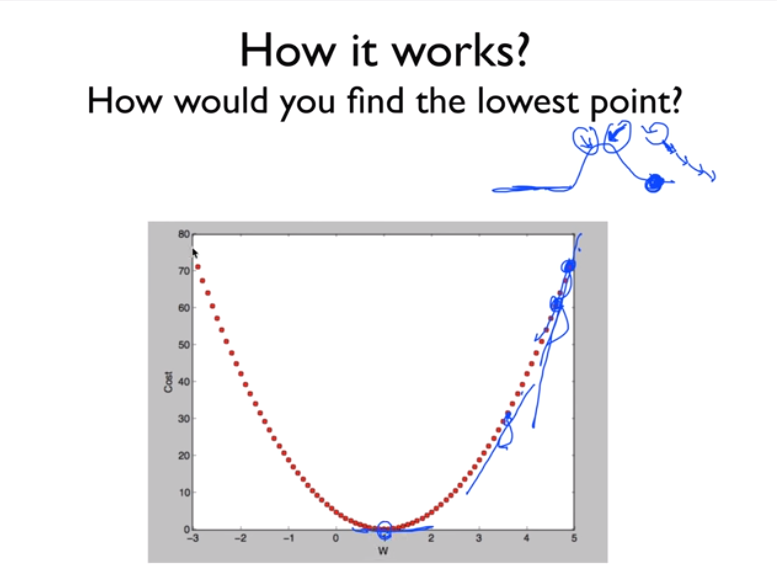
W에 따라 cost(W)가 어떻게 변할지 그래프를 그려볼 수 있다.

 

우리는 cost 함수가 최소화되게끔 찾아야 하기 때문에 최소화된 점을 찾는다. 

여기선 (1,0)이지만 기계적으로 찾아야 한다.

 

최솟값을 찾을 때 많이 사용되는 알고리즘이 경사하강법 Gradient descent algorithm이다.

만약 언덕 위에 있다면 주변에 있는 경사진 곳을 찾아 내려가는 간단한 방식이다.
그래프의 경사도에 따라 움직여 내려가고 경사도가 없는 점에 머무르게 된다. 

 

Gradient descent algorithm은 아무지점에서나 시작할 수 있다. 
원리는 W를 조금 바꾸고 cost 함수를 줄이는 것이다.
그 뒤 미분을 이용해 경사도를 계산하고, 계속해서 갱신과정을 반복한다.
어느 지점에서 시작하든 간에 최소점에 도달할 수 있다.

 

아래는 cost 함수 알고리즘을 일반화한 것으로, 1/m을 1/2m으로 수정한다. 

1/m 최소화나 1/2m 최소화나 두 함수 의미는 같다. 

 

그 뒤 공식적인 알고리즘은 다음과 같다.

W에 α(learning rate) 0.1정도의 상수 알파에 cost함수를 미분한 것(점의 기울기) 이다.

 

미분하는 절차다. 

여러번 실행시키고 W가 변화하면서 cost 함수가 최소화되는 W가 나온다.

https://www.derivative-calculator.net/ 미분을 계산해주는 웹사이트에서 쉽게 미분 결과를 얻을 수 있다.

 

한편, 아래 그래프는 시작점에 따라 도착점이 나뉘게 된다.

W 0.4, b 0.8의 값에 도달하는 경우와 W 0.3, b 0.2의 값에 도달하는 경우로 나뉜다. 
이런 방식이라면 알고리즘이 제대로 동작하지 않는다.

 

다행히 우리의 Hypothesis와 cost 함수는 다음과 같은 그래프를 만든다.

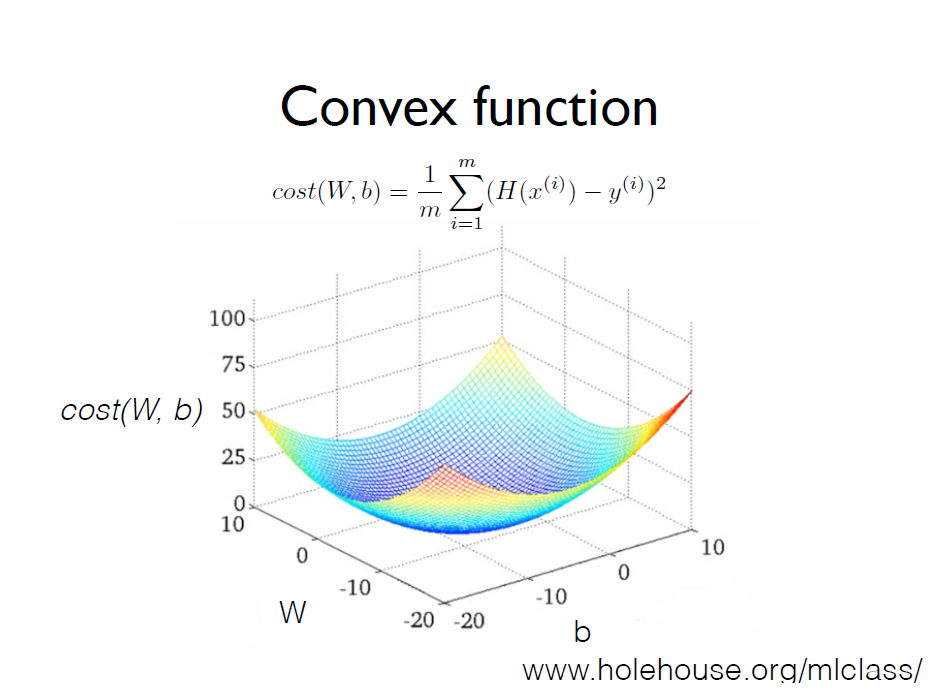
밥그릇 같은 오목한 모양이고, 이런 경우엔 어느 점에서 시작하든 같은 지점에 도달한다.

이것을 Convex function이라고 한다.

Linear Regression 적용 전 cost 함수를 설계할 때, 그래프의 모양이 Convex function이 되는지 반드시 확인해야 한다.

 

 

---

출처

김성훈 교수님의 강의 <모두를 위한 딥러닝>

시즌 1 - 딥러닝의 기본 (TF 1.X lab 완료!)

https://hunkim.github.io/ml/